newest Trough idlers-wholesale Trough idler support-Guobo

0
百度权重
0
百度移动
0
3 6 0权重
0
搜狗权重
热度
0
出站链接

网站编号：35050
所属分类：电影视频
加入时间：2025-03-20 14:01:59
网站备案: -

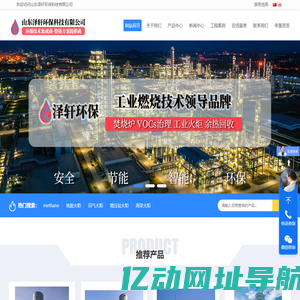
网站URL： https://www.hbgbmachine.com
预估IP流量：-
IP地址：- 地址：-
备案方: -

关键词：(51个字符)
newest、 Trough、 idlers、 wholesale、 Trough、 idler、 support、
网站简介：(112个字符)
GuoboMainbusinessnewestTroughidlers,wholesaleTroughidlersupport.Goodquality,richvarietyandcompletespecifications

网站截图/LOGO

上一篇：Bootstrap Portfolio Page Template | 下一篇：好好听故事网后台管理-登陆

在本站关于www.hbgbmachine.com说明：

www.hbgbmachine.com由网友主动性提交被亿动网址导航整理收录的，亿动网址导航仅提供www.hbgbmachine.com的基础信息并免费向大众网友展示，www.hbgbmachine.com的是IP地址：- 地址：-，www.hbgbmachine.com的百度权重为0、百度手机权重为0、百度收录为0条、360收录为0条、搜狗收录为0条、谷歌收录为0条、百度来访流量大约在-之间、百度手机端来访流量大约在-之间、www.hbgbmachine.com的备案号是-、备案人叫-、被百度收录的关键词有0个、手机端关键词有0个、迄今为止已经创建未知。

下载地址: txt下载、docx下载、pdf下载、rar下载、zip下载

本页地址: https://www.ed4.cn/links/88da3105c77a6e4e8fff.html

温馨提示

做上本站友情链接,在您站上点击一次,即可自动秒收录并自动排在本站第一位！
<a href="https://www.ed4.cn/" target="_blank">亿动网址导航</a>

SEO综合信息

SEO信息	百度来访IP：- \| 移动端来访IP：- \| 出站链接： \| 站内链接：0
IP网速：	IP地址：- 地址：- \| 网速：223毫秒
ALEXA排名	世界排名：- \| 预估IP：- \| 预估PV：-
备案信息	- \| 名称：- \| 已创建：未知

收录	百度	360	搜狗	谷歌
查询	0	0	0	0

电脑关键词	手机关键词	页面友好	首页位置	索引	近期收录
0	0	电脑端优秀	-	0	0

服务器信息协议类型 - 页面类型 - 服务器类型 - 程序支持 - 连接标识 - 消息发送 - GZIP检测 - 源文件大小 - 压缩后大小 - 压缩率 -

网页快照

              n e w e s t T r o u g h i d l e r s w h o l e s a l e T r o u g h i d l e r s u p p o r t G u o b o C o n v e y o r b e l t p r o d u c t s o l u t i o n s e x p e r t + 8 6 1 8 2 3 2 8 1 0 0 5 1 s a l e @ h b g b m a c h i n e . c o m l a n g u a g e l a n g u a g e H O M E C O M P A N Y C o m p a n y p r o f i l e P r o d u c t i o n A b i l i t y V i d e o P R O D U C T S I d l e r B a c k s t o p r o l l R o l l e r R o l l e r g r o u p B r a c k e t D S J d o w n h o l e r e t r a c t a b l e b e l t c o n v e y o r P R O J E C T S A p p l i c a t i o n C a s e S E R V I C E S e r v i c e G u a r a n t e e G l o b a l n e t w o r k B L O G C o m p a n y N e w s I n d u s t r y d y n a m i c s C O N T A C T U S C l o s e I n q u i r y T o t a l X C l e a r a l l G U O B O M A C H I N E R Y I d l e r m a n u f a c t u r e r s , p r o f e s s i o n a l c u s t o m i z a t i o n S t o p r o l l e r , s t a i n l e s s s t e e l r o l l e r , c o n e i d l e r l o w e r c o r e a s s e m b l y , q u a l i t y b r a c k e t , a l i g n i n g b r a c k e t , D S J d o w n h o l e t e l e s c o p i c b e l t c o n v e y o r b e l t . L e a r n M o r e → G U O B O M A C H I N E R Y R o l l e r m a n u f a c t u r e r c u s t o m i z e d o n d e m a n d T h e c o m p a n y h a s a n u m b e r o f a d v a n c e d r o l l e r p a r t s p r o d u c t i o n l i n e , a s w e l l a s e x p e r i e n c e d p r o f e s s i o n a l e n g i n e e r i n g a n d t e c h n i c a l p e r s o n n e l , s o p h i s t i c a t e d p r o d u c t i o n e q u i p m e n t a n d p e r f e c t t e s t i n g m e a n s . L e a r n M o r e → G U O B O M A C H I N E R Y R o l l e r m a n u f a c t u r e r , s u p p o r t f a c t o r y i n s p e c t i o n C h o o s e o u r p r o f e s s i o n a l r e s t a s s u r e d , s u p p o r t c u s t o m , t o v i s i t t h e f a c t o r y . L e a r n M o r e → s c r o l l d o w n S a f e A n d F a s t D e l i v e r y R e f u n d s G u a r a n t e e d D r o p S h i p p i n g F a n t a s t i c C u s t o m e r S e r v i c e W h a t W e O f f e r I d l e r B a c k s t o p r o l l R o l l e r R o l l e r g r o u p B r a c k e t S c r e w r o l l e r I t i s s u i t a b l e f o r t r a n s p o r t i n g c o a l i n f l a m m a b l e s i t u a t i o n s i n c o a l m i n e s , a n d c a n a l s o b e u s e d i n e l e c t r i c p o w e r , c h e m i c a l i n d u s t r y , m e t a l l u r g y a n d o t h e r i n d u s t r i e s r e q u i r i n g n o n f l a m m a b l e d e v i c e s t o c o n d u c t s t a t i c e l e c t r i c i t y . M o r e I n q u i r y C o n e t y p e r o l l e r I t i s s u i t a b l e f o r t r a n s p o r t i n g c o a l i n f l a m m a b l e s i t u a t i o n s i n c o a l m i n e s , a n d c a n a l s o b e u s e d i n e l e c t r i c p o w e r , c h e m i c a l i n d u s t r y , m e t a l l u r g y a n d o t h e r i n d u s t r i e s r e q u i r i n g n o n f l a m m a b l e d e v i c e s t o c o n d u c t s t a t i c e l e c t r i c i t y . M o r e I n q u i r y N y l o n i d l e r s e t I t i s s u i t a b l e f o r t r a n s p o r t i n g c o a l i n f l a m m a b l e s i t u a t i o n s i n c o a l m i n e s , a n d c a n a l s o b e u s e d i n e l e c t r i c p o w e r , c h e m i c a l i n d u s t r y , m e t a l l u r g y a n d o t h e r i n d u s t r i e s r e q u i r i n g n o n f l a m m a b l e d e v i c e s t o c o n d u c t s t a t i c e l e c t r i c i t y . M o r e I n q u i r y C u s h i o n r o l l e r I t i s s u i t a b l e f o r t r a n s p o r t i n g c o a l i n f l a m m a b l e s i t u a t i o n s i n c o a l m i n e s , a n d c a n a l s o b e u s e d i n e l e c t r i c p o w e r , c h e m i c a l i n d u s t r y , m e t a l l u r g y a n d o t h e r i n d u s t r i e s r e q u i r i n g n o n f l a m m a b l e d e v i c e s t o c o n d u c t s t a t i c e l e c t r i c i t y . M o r e I n q u i r y T r o u g h i d l e r s I t i s s u i t a b l e f o r t r a n s p o r t i n g c o a l i n f l a m m a b l e s i t u a t i o n s i n c o a l m i n e s , a n d c a n a l s o b e u s e d i n e l e c t r i c p o w e r , c h e m i c a l i n d u s t r y , m e t a l l u r g y a n d o t h e r i n d u s t r i e s r e q u i r i n g n o n f l a m m a b l e d e v i c e s t o c o n d u c t s t a t i c e l e c t r i c i t y . M o r e I n q u i r y N y l o n i d l e r I t i s s u i t a b l e f o r t r a n s p o r t i n g c o a l i n f l a m m a b l e s i t u a t i o n s i n c o a l m i n e s , a n d c a n a l s o b e u s e d i n e l e c t r i c p o w e r , c h e m i c a l i n d u s t r y , m e t a l l u r g y a n d o t h e r i n d u s t r i e s r e q u i r i n g n o n f l a m m a b l e d e v i c e s t o c o n d u c t s t a t i c e l e c t r i c i t y . M o r e I n q u i r y A l l P r o d u c t s G U O B O ® C o n v e y o r b e l t p r o d u c t s e r i e s s o l u t i o n s e x p e r t H e b e i G u o b o M a c h i n e r y M a n u f a c t u r i n g C o . , L t d . f o c u s e s o n t h e p r o d u c t i o n o f v a r i o u s t y p e s o f r o l l e r r o l l e r p r o d u c t s , c o v e r i n g r o l l e r s , p o l y m e r r o l l e r s , b u f f e r r o l l e r s , f r i c t i o n r o l l e r s , n y l o n r o l l e r s , p a r a l l e l r o l l e r s , t r o u g h r o l l e r s , c o n e r o l l e r s a n d o t h e r v a r i e t i e s . T h e c o m p a n y h a s a n u m b e r o f a d v a n c e d r o l l e r p a r t s p r o d u c t i o n l i n e s , a s w e l l a s e x p e r i e n c e d p r o f e s s i o n a l e n g i n e e r i n g a n d t e c h n i c a l p e r s o n n e l , s o p h i s t i c a t e d p r o d u c t i o n e q u i p m e n t a n d p e r f e c t t e s t i n g m e a n s t o e n s u r e t h a t e a c h p r o d u c t h a s b e e n c a r e f u l l y d e s i g n e d a n d s t r i c t i n s p e c t i o n . 2 0 y e a r s ’ P r o d u c t i o n e x p e r i e n c e 7 0 0 0 0 ㎡ C o m p a n y a r e a 1 5 0 + S t a f f a t p r e s e n t 8 0 + E x p o r t e d c o u n t r i e s V i e w M o r e I n d u s t r y S o l u t i o n s T h e c o m p a n y s p r o d u c t s a r e w i d e l y u s e d i n l o g i s t i c s , t r a n s p o r t a t i o n , c o n s t r u c t i o n , a g r i c u l t u r e a n d o t h e r f i e l d s , m a i n l y f o r s u p p o r t i n g a n d r o t a t i n g l a r g e w e i g h t o b j e c t s , m a k i n g i t e a s i e r t o m o v e . R o l l w i t h t h e B e s t : A D e e p D i v e i n t o M i n i n g R o l l e r P r o d u c t s T h e U n s u n g H e r o e s o f M i n i n g : U n d e r s t a n d i n g t h e W o r k i n g P r i n c i p l e s o f C o n v e y o r R o l l e r s D e m y s t i f y i n g M i n i n g R o l l e r s : A G u i d e t o C o m m o n Q u e r i e s U n v e i l i n g t h e V e r s a t i l e A p p l i c a t i o n s o f M i n i n g R o l l e r s R o l l i n g i n t o E f f i c i e n c y : T h e U n s u n g H e r o e s o f M i n i n g C o n v e y a n c e T h e B a c k b o n e o f M i n i n g : U n d e r s t a n d i n g t h e R o l e o f C o n v e y o r R o l l e r s R o l l i n g i n t o t h e F u t u r e : T h e R o l e o f M i n i n g I d l e r s i n I n d u s t r y S o l u t i o n s T h e B a c k b o n e o f M i n i n g : U n d e r s t a n d i n g t h e R o l e o f C o n v e y o r R o l l e r s R o l l w i t h t h e B e s t : A D e e p D i v e i n t o M i n i n g R o l l e r P r o d u c t s T h e U n s u n g H e r o e s o f M i n i n g : U n d e r s t a n d i n g t h e W o r k i n g P r i n c i p l e s o f C o n v e y o r R o l l e r s D e m y s t i f y i n g M i n i n g R o l l e r s : A G u i d e t o C o m m o n Q u e r i e s U n v e i l i n g t h e V e r s a t i l e A p p l i c a t i o n s o f M i n i n g R o l l e r s R o l l i n g i n t o E f f i c i e n c y : T h e U n s u n g H e r o e s o f M i n i n g C o n v e y a n c e T h e B a c k b o n e o f M i n i n g : U n d e r s t a n d i n g t h e R o l e o f C o n v e y o r R o l l e r s R o l l i n g i n t o t h e F u t u r e : T h e R o l e o f M i n i n g I d l e r s i n I n d u s t r y S o l u t i o n s T h e B a c k b o n e o f M i n i n g : U n d e r s t a n d i n g t h e R o l e o f C o n v e y o r R o l l e r s C o m p a n y S t r e n g t h C o m p a n i e s a d h e r i n g t o t h e q u a l i t y o f s u r v i v a l , c r e d i b i l i t y a n d d e v e l o p m e n t , s e r v i c e a n d e f f i c i e n c y , c u s t o m e r f i r s t b u s i n e s s p u r p o s e s , a l l p r o d u c t s a r e s t r i c t l y i n a c c o r d a n c e w i t h n a t i o n a l s t a n d a r d s a n d u s e r n e e d s f o r p r o d u c t i o n . S o u r c e m a n u f a c t u r e r s p r i c e i s r e a s o n a b l e P h y s i c a l f a c t o r y , s u p p o r t t o m a p t o s a m p l e c u s t o m i z a t i o n E x q u i s i t e w o r k m a n s h i p o f e x c e l l e n t q u a l i t y I n d u s t r y e x p e r i e n c e , q u a l i t y a s s u r a n c e S p o t i n v e n t o r y p r o f e s s i o n a l a f t e r s a l e s E x c e l l e n t a f t e r s a l e s , f o r y o u t o s o l v e d i f f i c u l t p r o b l e m s C u s t o m e r R e v i e w s F r e e c u s t o m i z e d s a m p l e s : w e p r o v i d e y o u w i t h p r o f e s s i o n a l s a m p l e p l a n s , 2 3 e x c e l l e n t s a m p l e c o l o r t e c h n i c i a n s s e r v e f o r y o u , s u c h a s w e d e s i g n t h i s l o g o f o r o u r G e r m a n c o m p a n y “ d e t a i l i n g . D e ” , t h e y a r e v e r y s a t i s f i e d w i t h o u r d e s i g n 。 
 I d l e r c u s t o m e r s e l l e r ★ ★ ★ ★ ★ F i n d a p r o f e s s i o n a l p r o d u c t i o n b u y e r i s a w o r r y , p r o d u c t q u a l i t y i s g o o d A u g 0 8 , 2 0 2 4 M i n i n g e q u i p m e n t b u y e r ★ ★ ★ ★ ★ M i n i n g e q u i p m e n t p r o f e s s i o n a l m a n u f a c t u r e r s , q u a l i t y s e r v i c e i s v e r y g o o d A u g 0 8 , 2 0 2 4 R u s s i a n c u s t o m e r ★ ★ ★ ★ ★ D e l i v e r y i s v e r y f a s t , t i m e l y d e l i v e r y a f t e r c o m m u n i c a t i n g w i t h t h e s e l l e r , w i t h o u t d e l a y , v e r y g o o d A u g 0 8 , 2 0 2 4 F A Q G u o b o M a c h i n e r y i s l o o k i n g f o r w a r d t o w o r k i n g w i t h m o r e c u s t o m e r s t o c r e a t e a b e t t e r f u t u r e . + 8 6 1 3 3 7 3 4 7 0 9 9 9 D e f i n i t i o n a n d c l a s s i f i c a t i o n o f r o l l e r s R o l l e r i s a n i m p o r t a n t p a r t o f b e l t c o n v e y o r , m a n y k i n d s , l a r g e q u a n t i t y , c a n s u p p o r t t h e c o n v e y o r b e l t a n d m a t e r i a l w e i g h t . R o l l e r i s a n i m p o r t a n t m e c h a n i c a l p a r t R o l l e r i s a n i m p o r t a n t m e c h a n i c a l p a r t , w i d e l y u s e d i n l o g i s t i c s , t r a n s p o r t a t i o n , c o n s t r u c t i o n , a g r i c u l t u r e a n d o t h e r f i e l d s . O n l i n e M e s s a g e F o r i n q u i r i e s a b o u t o u r p r o d u c t s , p l e a s e e m a i l t o u s a n d w e w i l l b e i n t o u c h w i t h i n 2 4 h o u r s .   h b g b m a c h i n e @ 3 0 0 . c n S u b m i t 5 0 0 m N o r t h o f F e n g c h i T u r n t a b l e , Y a n s h a n C o u n t y , C a n g z h o u C i t y , H e b e i P r o v i n c e , C h i n a + 8 6 1 8 2 3 2 8 1 0 0 5 1 s a l e @ h b g b m a c h i n e . c o m + 8 6 1 8 2 3 2 8 1 0 0 5 1 H O M E C O M P A N Y C o m p a n y p r o f i l e P r o d u c t i o n A b i l i t y V i d e o P R O D U C T S I d l e r B a c k s t o p r o l l R o l l e r R o l l e r g r o u p B r a c k e t D S J d o w n h o l e r e t r a c t a b l e b e l t c o n v e y o r P R O J E C T S A p p l i c a t i o n C a s e S E R V I C E S e r v i c e G u a r a n t e e G l o b a l n e t w o r k B L O G C o m p a n y N e w s I n d u s t r y d y n a m i c s C O N T A C T U S P o w e r b y : 3 0 0 . c n | T a g   |   C i t y L i s t 丨 P r i v a c y P o l i c y B u s i n e s s L i c e n s e

站点推荐

食品级板式换热器_天津板式换热器_板式换热器胶条_板式冷却器_天津博泰换热设备有限公司

天津博泰换热设备有限公司是板式换热器生产厂家,板式换热器公司主营食品级板式换热器,天津板式换热器,汽水板式换热器,板式换热器密封垫,钛材板式换热器,全焊式板式换热器,板式换热机组,板式冷却器等产品.是一家生产板式换热器及板式换热器板片的企业，工厂占地面积25000平方米，拥有40000T,15000T、10000T、8000T、6000T等大型压机10余台，大型冲剪设备10余台，数控切割、激光切割、激光焊接等一大批先进的生产设备。

大楚资讯 - 武汉本地生活指南

大楚资讯专注于为武汉提供新闻热点、生活、办事、汽车、科技、教育、时尚、房产、旅游等栏目资讯内容。

心逸酒店集团

暂无描述...

乳胶枕头|乳胶被|乳胶凉席-江苏雅诗妮床垫有限公司

江苏雅诗妮床垫有限公司专业生产乳胶枕头,乳胶被,乳胶凉席,是乳胶床垫厂家,乳胶枕头厂家,是乳胶凉席产品的研究以及生产.我们真诚期待与您的合作,携手共创美好的明天.

票根-票根网-收费公路通行费增值税电子发票服务系统

暂无描述...

北京_叉车租赁,租赁叉车,出租叉车,叉车出租,叉车租赁公司,租赁叉车公司,出租叉车公司,叉车出租公司-北京宏金伟业机械设备有限公司

北京宏金伟业机械设备有限公司是北京及周边地区开展叉车业务技术全面的一家综合性服务公司，下设很多直销处及一个修理工厂。10年以上资深人员有8人，维修场地面800m2。全新叉车样机通常保持在20辆左右，二手叉车30-50辆。　

个人测试开发

暂无描述...

吴起吧小站

吴起-吴起123-吴起微城-吴起信息网-吴起吧-郑喜明

液压扳手|液压扳手泵|螺栓拉伸器,PRIMO普锐马

PRIMO普锐马液压扳手,专业扭矩工具厂家,为风电,火电,石油化工,机械制造,钢结构等行业螺栓预紧提供专业预紧产品及工程技术服务,产品通过ISO9001/CE认证,服务国内外风电、石化、机械制造等龙头企业,产品畅销全球，电话：021-51028700.液压扳手又称液压扭矩扳手|液压扭力扳手,分为驱动轴液压扳手和中空液压扳手。